 | How to disable the autorun function (autorun.inf)Windows |
Disabling the autorun function in Windows XP
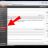
Click on the Start button and then click on Run. In the Run window type gpedit.msc and then press Enter. The Group Policy window will appear on the screen.
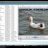
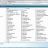
From the left column open Administrative Templates (1 on the image below) and then choose System (2 on the image below).
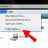
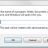
On the list from the right, double click on Turn off Autoplay (3 on the image below). Now you will need to click on Enabled (4 on the image below), and from the list choose All drives (5 on the image below).
Click on OK and you’re done.
Disable the autorun function on Windows 7 and Vista
Click on Start and type gpedit.msc in the search field and the press Enter. The Group Policy Editor window will appear.
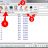
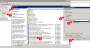
From the left column, click on Administrative Templates (1 on the image below), the on Windows Components (2 on the image below) and on AutoPlay policies (3 on the image below).
From the right column double click on Turn off Autoplay (4 on the image below), click on Enabled (5 on the image below) and then choose All drives from the list (6 on the image below).
Click on OK and you are done.
Read more from Windows |



 HOME
HOME CATEGORIES
CATEGORIES CONTACT
CONTACT